The Gauss Code of a Link

Below we describe how to input a knot or a link if you have its planar diagram and crossing behavior. The diagram must be connected and have at least one crossing. We use an encoding which is a little different from what is usually called Gauss code, providing additional information that allows to distinguish knots from their mirror images.

1. For each component, choose an orientation and a starting point.
2. Assign different indices, which must be natural numbers, to all the crossings.
3. For each connected component, go along it starting from the marked point in the chosen direction, and each time you come through a crossing, write down the index of the crossing preceded by two symbols: the first one must be + or - indicating whether you go over or under the crossing, and the second must be  >  or  <  sign indicating whether you see the arc that you intersect going from left two the right or from right to the left, respectively. Entries for different crossings must be separated by spaces.
4. When you come back to the starting point of the chosen component, proceed with the next one. Separate entries for different components by keyword "component".

For example, for the picture below you get the following Gauss code:

->5 +<6

component

+<5 ->6 ->4 +<3 -<1 +>2 ->3 +<4 -<2 +>1

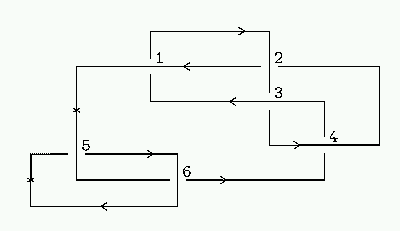
Example of a Link and Gauss Code

Here is real world example of a knot encoded as Gauss code: 10.1.gc